台形
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(2012年9月) |
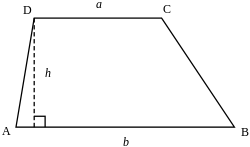
台形
台形(だいけい、米: trapezoid、英: trapezium)は、四角形の一部で、少なくとも一組の対辺が互いに平行であるような図形である。平行な2本の対辺を台形の底辺といい、そのうち一方を上底(じょうてい)、他方を下底(かてい)とよぶ。また、もう一組の対辺を台形の脚(きゃく)とよぶ。
台形のうち、下底の両端にある2つの内角(底角)の大きさが互いに等しいとき、上底の両端にある2つの底角も互いに等しくなる。このような台形を等脚台形という。等脚台形は線対称な図形であり、その対称軸は2本の底辺それぞれの中点をともに通る。
台形のうち、台形の脚もまた平行となっているとき、すなわち対辺が2組ともそれぞれ平行であるような四角形は平行四辺形とよばれる。平行四辺形は台形の特殊な形と考えられる。平行四辺形は点対称な図形であり、その対称の中心は対角線の交点に等しい。
台形を対角線の1本を境に分割すると2つの三角形になるがその三角形の面積比は上底と下底の長さの比に等しい。これは分割によって高さ(台形の場合は上底と下底の間の距離)の等しい三角形が2つできるためである。
台形を2本の対角線で分割すると4つの三角形になるが、台形の底辺を辺に持つ2つの三角形の面積比は上底と下底の長さの比の平方に等しい。これは分割によって相似な三角形ができるためである。また、台形の脚を辺に持つ2つの三角形の面積は互いに等しく、それらはともに、台形の底辺を辺に持つ2つの三角形の面積の相乗平均に等しい。
台形の面積 S の公式でよく知られているものは
- S=(a+b)h2{displaystyle S={frac {(a+b)h}{2}}}
である。ここに a, b, h は上底、下底、高さに対応する長さである。用語で表現するなら(上底 + 下底)×(高さ)÷ 2 である。この公式は、台形を対角線で2つに分けたときの各々の三角形の面積が ah/2 および bh/2 であることから得られる。この公式を導く別の方法としては、まず2つの台形を上底と下底以外の辺(上図での AD もしくは BC)同士を重ね合わせて平行四辺形をつくる。そしてその平行四辺形の面積(=(底辺)×(高さ))は (a + b)h であり、その半分が台形の面積にあたるので S = (a + b)h/2 が導かれる。a = 0 とおくと底辺 b の三角形の面積に等しい。
4本の辺の長さ x, y, z, w が分かっている場合は以下の式で台形の面積を求めることもできる。
- S=x+z4(x−z)(x+y−z+w)(x−y−z+w)(x+y−z−w)(−x+y+z+w){displaystyle S={frac {x+z}{4(x-z)}}{sqrt {(x+y-z+w)(x-y-z+w)(x+y-z-w)(-x+y+z+w)}}}
ただし x と z は平行で x は z よりも長い辺とする。x = z ならばその台形は平行四辺形である。

台形の面積で定積分を近似する
積分の数値計算ではグラフ上のある区間の面積
- ∫abf(x)dx{displaystyle int _{a}^{b}f(x)dx}
を求めるために、x 軸、x = a、x = b とグラフで囲まれた図形を有限個の(できるだけ多い)台形で分割し、台形の面積の公式を用いて近似値を得ることがある。台形公式を参照のこと。
関連項目
- 四角形
- 等脚台形
- 平行四辺形
- 数値計算
| ||||||||||||


