一般相対性理論





物理学 > 相対性理論 > 一般相対性理論



質量（地球）が2次元で描いた格子模様の平面に落とし込んだ状態を描いた説明図。その説明図から見てもわかるように、格子模様をゆがめている様子が視認出来、なおかつ歪んでいる格子模様自体が重力と解釈できる。この説明図を一般人にも理解できるよう例えるなら、重い物がトランポリンに沈む状態と同じである。










一般相対性理論

Gμν+Λgμν=8πGc4Tμν{displaystyle G_{mu nu }+Lambda g_{mu nu }={tfrac {8pi G}{c^{4}}}T_{mu nu }}{displaystyle G_{mu nu }+Lambda g_{mu nu }={tfrac {8pi G}{c^{4}}}T_{mu nu }}


アインシュタイン方程式

入門（英語版）
数学的定式化
関連書籍



























表・話・編・歴


一般相対性理論（いっぱんそうたいせいりろん、独: allgemeine Relativitätstheorie, 英: general theory of relativity）は、アルベルト・アインシュタインが1905年の特殊相対性理論に続いて1915年から1916年にかけて発表した物理学の理論である。一般相対論（いっぱんそうたいろん、英: general relativity）とも。




目次






  • 1 概要


  • 2 歴史


    • 2.1 一般相対性理論が成立するまでの研究


    • 2.2 一般相対性理論の発表後




  • 3 物理学としての位置づけ


    • 3.1 万有引力の法則との関係


    • 3.2 特殊相対性理論との関係


    • 3.3 量子力学との関係


      • 3.3.1 曲がった時空上の場の理論 (Quantum field theory in curved spacetime)


      • 3.3.2 超弦理論






  • 4 一般相対性理論の内容


    • 4.1 時空モデルとしてのリーマン多様体に求められる条件


    • 4.2 測地線の方程式


    • 4.3 リーマンテンソル、アインシュタイン・テンソル


    • 4.4 アインシュタイン方程式とその特徴


    • 4.5 アインシュタイン方程式の厳密解




  • 5 一般相対性理論の応用


    • 5.1 GNSS




  • 6 脚注


    • 6.1 注釈


    • 6.2 出典




  • 7 参考文献


  • 8 関連文献


  • 9 関連項目


  • 10 外部リンク





概要




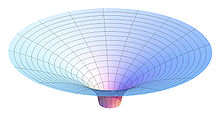
重力場の概念図。中心に近づくほど重力が大きい。


一般相対性原理と一般共変性原理および等価原理を理論的な柱とし、リーマン幾何学を数学的土台として構築された古典論的な重力場の理論であり、古典物理学の金字塔である[注 1]。測地線の方程式とアインシュタイン方程式（重力場の方程式）が帰結である。時間と空間を結びつけるこの理論では、アイザック・ニュートンによって万有引力として説明された現象が、もはやニュートン力学的な意味での力ではなく、時空連続体の歪みとして説明される。


一般相対性理論では、次のことが予測される。



重力レンズ効果

重力場中では光が曲がって進むこと。アーサー・エディントンは、1919年5月29日の日食で、太陽の近傍を通る星の光の曲がり方がニュートン力学で予想されるものの2倍であることを観測で確かめ、一般相対性理論が正しいことを示した。


水星の近日点の移動

ニュートン力学だけでは、水星軌道のずれ（近日点移動の大きさ）の観測値の説明が不完全だったが、一般相対性理論が解決を与え、太陽の質量による時空連続体の歪みに原因があることを示した。

重力波


時空の歪み（重力場）の変動が伝播する現象。線型近似が有効な弱い重力波の伝播速度は光速である。アインシュタインによる予測の発表から100年目の2016年に、アメリカのLIGOにより直接観測された。

膨張宇宙

時空は膨張または収縮し、定常にとどまることがないこと。ビッグバン宇宙を導く。

ブラックホール

限られた空間に大きな質量が集中すると、光さえ脱出できないブラックホールが形成される。


重力による赤方偏移

強い重力場から放出される光の波長は元の波長より引き延ばされる現象。


時間の遅れ

強い重力場中で測る時間の進み（固有時間）が、弱い重力場中で測る時間の進みより遅いこと。


一般相対性理論は慣性力と重力を結び付ける等価原理のアイデアに基づいている。等価原理とは、簡単に言えば、外部を観測できない箱の中の観測者は、自らにかかる力が、箱が一様に加速されるために生じている慣性力なのか、箱の外部にある質量により生じている重力なのか、を区別することができないという主張である。


相対論によれば空間は時空連続体であり、一般相対性理論では、その時空連続体が均質でなく歪んだものになる。つまり、質量が時空間を歪ませることによって、重力が生じると考える。そうだとすれば、大質量の周囲の時空間は歪んでいるために、光は直進せず、また時間の流れも影響を受ける。これが重力レンズや時間の遅れといった現象となって観測されることになる。また質量が移動する場合、その移動にそって時空間の歪みが移動・伝播していくために重力波が生じることも予測される。


アインシュタイン方程式から得られる時空は、ブラックホールの存在や膨張宇宙モデルなど、アインシュタイン自身さえそれらの解釈を拒むほどの驚くべき描像である。しかし、ブラックホールや初期宇宙の特異点の存在も理論として内包しており、特異点の発生は一般相対性理論そのものを破綻させてしまう。将来的には量子重力理論が完成することにより、この困難は解決されるものと期待されている。



歴史



一般相対性理論が成立するまでの研究


1905年に特殊相対性理論を発表したアインシュタインは、特殊相対性理論を加速度運動を含めたものに拡張する理論の構築に取り掛かった。1907年に、アインシュタイン自身が「人生で最も幸福な考え (the happiest thought of my life)」と振り返る「重力によって生じる加速度は観測する座標系によって局所的にキャンセルすることができる」というアイディア（等価原理[1]）を得る。 光の進み方と重力に関する論文を1911年に出版した後、1912年からは、重力場を時空の幾何学として取り扱う方法を模索した。このときにアインシュタインにリーマン幾何学の存在を教えたのが、数学者マルセル・グロスマンであった。ただし、このときグロスマンは、「物理学者が深入りする問題ではない」と助言したとも伝えられている。1915年-16年には、これらの考えが1組の微分方程式（アインシュタイン方程式）としてまとめられた。


この時期にアインシュタインが発表した一般相対性理論に関する論文は、以下の通り。



  • 1911年 論文『光の伝播に対する重力の影響[注 2]』(Annalen der Physik, 35, 898-908)

  • 1914年 論文『一般相対性理論および重力論の草案[注 3]』(ZS. f. Math. u. Phys., 62, 225-261)

  • 1915年 論文『水星の近日点の移動に対する一般相対性理論による説明[注 4]』(S.B. Preuss. Akad. Wiss., 831-839)

  • 1916年 論文『一般相対性理論の基礎[注 5]』(Annalen der Physik (Germany), 49, 769-822)

  • 1916年 論文『ハミルトンの原理と一般相対性理論[注 6]』(S.B. Preuss. Akad. Wiss., 1111-1116)



一般相対性理論の発表後


アインシュタイン方程式の発表後は、その方程式を解くことが研究の課題となった。


1916年にカール・シュヴァルツシルトが、アインシュタイン方程式を球対称・真空の条件のもとに解き、今日ブラックホールと呼ばれる時空を表すシュヴァルツシルト解を発見した。アインシュタイン自身は、自ら導いた方程式から、重力波の概念を提案したり、宇宙全体に適用すると動的な宇宙が得られてしまうことから、宇宙項を新たに方程式に加えるなどの提案を行っている。



  • 1917年 論文『一般相対性理論についての宇宙論的考察』(S.B. Preuss. Akad. Wiss., 142-152)

  • 1918年 論文『重力波について』(S.B. Preuss. Akad. Wiss., 154-167)




1919年5月29日の皆既日食の写真。アーサー・エディントンが撮影した。


1919年5月19日にアーサー・エディントンが皆既日食を利用して、一般相対性理論により予測された太陽近傍での光の曲がりを確認したことにより、理論の正しさが認められ、世間への認知が一気に広まった。


1922年には、宇宙膨張を示唆するフリードマン・ロバートソンモデルが提案されるが、アインシュタイン自身は、宇宙が定常であると信じていたので、現実的な宇宙の姿であるとは受け入れようとはしなかった。


しかし、1929年には、エドウィン・ハッブルが、遠方の銀河の赤方偏移より、宇宙が膨張していることを示し、これにより、一般相対性理論の予測する時空の描像が正しいことが判明した。後にアインシュタインは宇宙項の導入を取り下げ、「生涯最大の失敗だった (the biggest blunder in my career)」とジョージ・ガモフに語ったという。


1931年、スブラマニアン・チャンドラセカールは、白色矮星の質量に上限があることを理論的計算によって示した。今日、チャンドラセカール限界として知られる式は、万有引力定数 G、プランク定数 h、光速 c の3つの基本定数を含み、古典物理・量子物理双方の成果を集大成したものでもある。チャンドラセカールは、「星の構造と進化にとって重要な物理的過程の理論的研究」の功績でノーベル物理学賞（1983年）を受賞した。


1939年、ロバート・オッペンハイマーとゲオルグ・ヴォルコフ (George Volkoff) は、中性子星形成のメカニズムを考察する過程で、重力崩壊現象が起きることを予測した。


その後しばらく、一般相対性理論は、「数学的産物」として実質的な物理研究の主流からは外れている。


重力波は果たして物理的な実体であるのかどうかという論争や、アインシュタイン方程式の厳密解の分類方法などの研究がしばらく続くが、1960年代のパルサーの発見やブラックホール候補天体の発見、そしてロイ・カーによる回転ブラックホール解（カー解）の発見を契機に、一般相対性理論は天文学の表舞台に登場する。同時期に、スティーヴン・ホーキングとロジャー・ペンローズが特異点定理を発表し、数学的・物理的に進展を始めると共に、ジョン・ホイーラーらが、古典重力・量子重力双方に物理的な描像を次々と提出し始めた。ワームホール（1957年）やブラックホール（1967年）という名前を命名したのは、ホイーラーである。


1974年、ジョゼフ・テイラーとラッセル・ハルスは、連星パルサー PSR B1913+16 を発見した。連星の自転周期とパルスの放射周期を精密に観測することによって、重力波 により、連星系からエネルギーが徐々に運び去られていることを示し、重力波の存在を間接的に証明した。この業績により、2人は「重力研究の新しい可能性を開いた新型連星パルサーの発見」としてノーベル物理学賞（1993年）を受賞した。


現在は、重力波の直接観測を目指して、世界各地でレーザー干渉計が稼働している。観測目標としている対象物は、中性子星連星やブラックホール連星の合体で生じる重力波などであり、波形の予測のための理論や数値シミュレーションが研究の重要な解決手段にもなっている。


また、宇宙論研究では、ビッグバン宇宙モデル（1947年）が有力とされているが、さらにその初期宇宙の膨張則を修正したインフレーション宇宙モデル（1981年）も正しいことが、2006年のWMAP衛星による宇宙背景輻射の観測により決定的になったと考える人も多い。最近は、高次元宇宙モデルが脚光を浴びているが、これらの宇宙モデルは、いずれも一般相対性理論を基礎にして議論される。


アインシュタイン以後、一般相対性理論以外の重力理論も、数多く提案されているが、現在までにほとんどが過去の観測結果を照合した上で棄却されている。実質的に対抗馬となるのは、カール・ブランスとロバート・H・ディッケによるブランス・ディッケ重力理論であるが、現在の観測では、ブランス・ディッケ理論のパラメーターは、ほとんど一般相対性理論に近づけなくてはならず、両者を区別することが難しいほどである。量子論と一般相対論の統一という物理学の試みは未だ進行中であるものの、一般相対性理論を積極的に否定する観測事実・実験事実は一つもない。他に提案されたどの重力理論よりも一般相対性理論は単純な形をしていることから、重力は一般相対性理論で記述される、と考えるのが現代の物理学である。



物理学としての位置づけ



万有引力の法則との関係


アインシュタイン方程式は微分方程式として与えられているため局所的な理論ではあるが、ちょうど電磁気学における局所的なマクスウェル方程式から大域的なクーロンの法則を導くことができるように、アインシュタイン方程式は静的なニュートンの万有引力の法則を包含している。万有引力の法則との主な違いは次の3点である。




  1. 重力は瞬時に伝わるのではなく光と同じ速さで伝わる。


  2. 重力から重力が発生する（非線形相互作用）。


  3. 質量を持つ物体の加速運動により重力波が放射される。


ここで、3.は荷電粒子が加速運動することにより電磁波が放射されることと類似している。これは、万有引力の法則やクーロンの法則に、運動する対象の自己の重力や電荷の効果を取り入れていることに対応している。



特殊相対性理論との関係


後述するように、一般相対性理論における時空間は数学的には各点の接ベクトル空間にミンコフスキー計量をいれた4次元多様体（ローレンツ多様体）で、アインシュタイン方程式を満たすものである。


よって各点の接ベクトル空間は、特殊相対性理論に従うミンコフスキー空間であり、接ベクトル空間とは、数学的にはテイラー展開の一次の項に対応している。


これはすなわち、一般相対性理論の側からみた場合、特殊相対性理論とは時空間上に任意に固定された一点の近傍において、一般相対性理論を一次近似したものである事を意味している。なお、（宇宙項のない）アインシュタイン方程式に登場する各項（曲率やエネルギー・運動量テンソル）は、二次の微分に関わる項であり、一次近似である特殊相対性理論には登場しない。


逆に特殊相対性理論の側から一般相対性理論をみると、特殊相対性理論の数学的定式化であるミンコフスキー空間は、全ての点に同一のミンコフスキー計量をいれた平坦なローレンツ多様体である。


このローレンツ多様体上では曲率は全点でゼロであるので、この事実を（宇宙項のない）アインシュタイン方程式に代入すると、この空間ではエネルギー・運動量テンソルがゼロである事を意味する。


また、平坦なローレンツ多様体上では共変微分と通常の微分は一致するので、全ての線形座標でクリストッフェル記号は消えている。クリストッフェル記号は物理学的には重力に対応しているので、これはすなわち全ての線形座標で重力がゼロである事を意味する。


以上より特殊相対性理論とは、エネルギー・運動量テンソルの影響が無視できる程度に、すなわち宇宙全体に比べれば微小な領域における理論であり、空間の曲率も領域の微小さゆえに無視できる場合の理論であると言える。



量子力学との関係


詳細は「量子重力理論」を参照

量子論は一般相対性理論と同様に物理学の基本的な理論の1つであると考えられている。しかし、一般相対性理論と量子論を整合させた理論（量子重力理論）はいまだに完成していない。現在、人類の知っているあらゆる物理法則は全て場の量子論と一般相対性理論という2つの理論から導くことができる。そのため、その2つを導くことのできる量子重力理論はこの世のすべてを説明できる万物の理論とも呼ばれている。


基本的に相対性理論で取り扱われる重力は、4つの基本相互作用のうち他の3つの力に比べて圧倒的に小さく、天体物理学や天文学で取り扱う天文現象のような巨視的（英語版）なレベル以下の大きさでは無視できる。逆に、量子論効果は量子化学や量子力学、素粒子物理学で取り扱う分子や原子、クォークなどのような微視的なレベル以上の大きさでは無視できる。よって相対性理論を適用する場面と量子論を適用する場面は重ならないためほとんどの場合この両者を考慮する必要はない。しかし、ブラックホールやビッグバンなどの大質量かつ微視的なスケールの現象を説明するためにはこの両者を併用する必要があるが、相対論と量子論を従来用いられてきた摂動法を用いて統合しようとすると、両者の間に深刻な対立が生じてしまい、並立させることが出来ない。従来の量子論では摂動展開時に生じる紫外発散（英語版）を繰り込みによって解消しているが、重力にはこの手法が適用できないのである。


この2つの理論の対立を折衷する様々な意見やその立証が試みられているが、未だ決定的な理論は出てきていない。



曲がった時空上の場の理論 (Quantum field theory in curved spacetime)


一般に場の量子論においては平坦なミンコフスキー時空における粒子を扱うが、重力の効果を近似的（半古典的）に背景時空（曲がった時空）として導入することにより、場の量子論に曲がった時空の効果を近似的に取り入れた理論である。


重力子の影響を背景時空として近似しているため、強い重力場のもとでは時空を完全に量子化したような量子重力理論に修正されるべきである。欠点としては、時空が静的なものであるため完全には相対論的ではない。


ホーキング放射はこの理論のもとで予測された。



超弦理論


詳細は「超弦理論」を参照

超弦理論は、従来の量子論では大きさを持たない点と仮定されている粒子を、長さを持つひもと仮定しなおすことにより紫外発散の問題を解消している。理論的な探求は進んでいるものの、実験的裏付けが非常に乏しく未だ仮説の域を脱していない。



一般相対性理論の内容


一般相対性理論は、次の仮定を出発点にする。あくまでも仮定であり、これが基準点とするるものではない。



一般相対性原理

物理学の法則は、任意の仕方で運動している座標系に関していつも成立する[2]

一般共変性の仮定

自然の一般法則[注 7]は、すべての座標系に対して成り立つ、すなわち任意の座標系に対して（一般）共変な方程式で表されなくてはならない[3]。

局所座標系における特殊相対性理論の成立仮定

無限に小さな4次元領域（4次元の擬リーマン多様体のある点における局所座標系または接空間）に対しては、座標を適当に選べば、特殊の意味での相対性理論が原則として成り立つ[注 8]。時空のある点における基本計量テンソル gi j は、その座標系に関する重力場を記述する[5]。基本計量テンソルの行列式 g は常に有限の負の値を持つ[6]。





測地線の仮定

自由質点運動は測地線である


一般相対性理論成立の歴史上、等価原理 (equivalence principle) はスタートポイントとして考えられたが、数学的に重要であるのは、一般相対性原理（一般共変性の仮定と局所座標系における特殊相対性理論の成立仮定）である。



時空モデルとしてのリーマン多様体に求められる条件


一般相対性理論においては、重力のある空間を光が通過するとき光は曲がる（光のとる経路が伸びる）ことから、時空は、重力場を基本計量テンソルとする4次元のリーマン多様体として扱われる[注 9]。可微分多様体 M がリーマン多様体であるとは、M 上の各点に基本計量テンソル gij(x) が与えられているものを言う。なお、局所座標系 (x0, x1, x2, x3) の四つの座標の内、x0 は適当な測定単位で測られた時間座標、x1, x2, x3 は空間座標とする。すなわち、x0 = ct, x1 = x, x2 = y, x3 = z であるとする。さらに、リーマン多様体上に定義されるテンソル概念に対して、上下に現れる同じ添字については常に和を取るというアインシュタインの縮約記法を用いる。


一般共変性の仮定

リーマン多様体を導入することで、一般共変性の仮定は、



ある自然の一般法則がある座標系で一つのテンソルの成分がすべてゼロになる形で書き表すことができるとき、すなわち、


（テンソルの成分） ＝ 0

とできるとき、その法則は一般共変性を持つ



というように、リーマン多様体上で定義されるテンソル概念の性質として定式化できるようになる。


局所座標系における特殊相対性理論の成立仮定

リーマン幾何学によれば、リーマン多様体上の無限に近い2点間の距離 ds は


ds2=gijdxidxj{displaystyle ds^{2}=g_{ij}dx^{i}dx^{j}}ds^{2}=g_{ij}dx^{i}dx^{j}

の平方で与えられる。この ds を4次元空間の無限に近い点に属する線素 (line element) の大きさと呼ぶ[7]が、これは、特殊相対性理論が成り立つような座標系においては、ミンコフスキーが指摘した4次元空間における不変量


ds2=c2dt2−dx2−dy2−dz2{displaystyle ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}}ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}

一致するものでなくてはならない。すなわち、適当な座標変換により、計量テンソル gij は、



gtt=1, gxx=gyy=gzz=−1{displaystyle g_{tt}=1,~g_{xx}=g_{yy}=g_{zz}=-1}g_{tt}=1,~g_{xx}=g_{yy}=g_{zz}=-1[注 10]

行列形式で描けば、


(10000−10000−10000−1){displaystyle {begin{pmatrix}1&0&0&0\0&-1&0&0\0&0&-1&0\0&0&0&-1\end{pmatrix}}}{begin{pmatrix}1&0&0&0\0&-1&0&0\0&0&-1&0\0&0&0&-1\end{pmatrix}}

となることが要請される。これはより一般的な表現として、有限で常に負の値をもつ基本計量テンソルの行列式 g = det(gij) に対する次の条件


−g=1{displaystyle {sqrt {-g}}=1}{sqrt {-g}}=1

という形で条件として求められる。



測地線の方程式


擬リーマン空間における測地線 (geodesic) は、通常の計量空間における定義と同様に、2点間の長さを最小にする曲線として定義される。曲線の長さは、



l(γ)=∫γ±gμνdxμdxν=∫γ±gμνdxμdtdxνdtdt{displaystyle l(gamma )=int _{gamma }{sqrt {pm g_{mu nu }dx^{mu }dx^{nu }}}=int _{gamma }{sqrt {pm g_{mu nu }{frac {dx^{mu }}{dt}}{frac {dx^{nu }}{dt}}}},dt}l(gamma )=int _{gamma }{sqrt {pm g_{mu nu }dx^{mu }dx^{nu }}}=int _{gamma }{sqrt {pm g_{mu nu }{frac {dx^{mu }}{dt}}{frac {dx^{nu }}{dt}}}},dt



で与えられる。ここでの積分は、曲線 γ(t) に沿うものとする。ルート内の符号の+は空間的な曲線に対して、負の符号は時間的な曲線に対して適用し、いずれの場合も長さが実数になるようにする。


この長さの極値をもたらす条件を導出すると、測地線の方程式が得られる。局所座標で表現すると、方程式は、



d2xμdt2+Γ νρμdxνdtdxρdt=0{displaystyle {frac {d^{2}x^{mu }}{dt^{2}}}+Gamma _{~nu rho }^{mu }{frac {dx^{nu }}{dt}}{frac {dx^{rho }}{dt}}=0}{frac {d^{2}x^{mu }}{dt^{2}}}+Gamma _{~nu rho }^{mu }{frac {dx^{nu }}{dt}}{frac {dx^{rho }}{dt}}=0



となる。ここで、xμ(t) は、曲線 γ(t) の座標であり、Γμ
 νρ  は先に登場したクリストッフェル記号である。座標の常微分方程式として得られるこの式は、初期値と初速度を与えれば解を一意に決定する。この式は、曲がった時空における光・粒子の運動方程式である。



リーマンテンソル、アインシュタイン・テンソル


時空の曲率は、レヴィ・チビタ接続 ∇ が定義するリーマン曲率テンソル (Riemann tensor) R ρ
 σμν  で表現される。局所座標表現では、次のように書ける。



Rρσμν=∂∂xμΓρνσ−∂∂xνΓρμσ+ΓρμλΓλνσ−ΓρνλΓλμσ{displaystyle {R^{rho }}_{sigma mu nu }={frac {partial }{partial x^{mu }}}Gamma ^{rho }{}_{nu sigma }-{frac {partial }{partial x^{nu }}}Gamma ^{rho }{}_{mu sigma }+Gamma ^{rho }{}_{mu lambda }Gamma ^{lambda }{}_{nu sigma }-Gamma ^{rho }{}_{nu lambda }Gamma ^{lambda }{}_{mu sigma }}{R^{rho }}_{sigma mu nu }={frac {partial }{partial x^{mu }}}Gamma ^{rho }{}_{nu sigma }-{frac {partial }{partial x^{nu }}}Gamma ^{rho }{}_{mu sigma }+Gamma ^{rho }{}_{mu lambda }Gamma ^{lambda }{}_{nu sigma }-Gamma ^{rho }{}_{nu lambda }Gamma ^{lambda }{}_{mu sigma }



物理的には、このリーマン曲率テンソルから、2成分を縮約したリッチテンソル (Ricci tensor) Rμν と、さらに添字を縮約したリッチスカラー曲率 (Ricci scalar) R



Rμν=Rρμρν{displaystyle R_{mu nu }={R^{rho }}_{mu rho nu }}R_{mu nu }={R^{rho }}_{mu rho nu }


R=gμνRμν{displaystyle R_{}^{}=g^{mu nu }R_{mu nu }}R_{}^{}=g^{mu nu }R_{mu nu }



を考えればよく、さらにその組み合わせである、



Gμν=Rμν−12Rgμν{displaystyle G_{mu nu }=R_{mu nu }-{frac {1}{2}}Rg_{mu nu }}G_{mu nu }=R_{mu nu }-{frac {1}{2}}Rg_{mu nu }



が物質分布で定まることをアインシュタインが見いだした。この最後の組み合わせ Gμν をアインシュタイン・テンソル (Einstein tensor) と呼ぶ。



アインシュタイン方程式とその特徴


一般相対性理論の基本方程式は、



Gμν+Λgμν=κTμν{displaystyle G_{mu nu }+Lambda g_{mu nu }=kappa T_{mu nu }}G_{mu nu }+Lambda g_{mu nu }=kappa T_{mu nu }



と表され、アインシュタイン方程式と呼ばれる。ここで Gμν はアインシュタインテンソル、gμν は計量テンソル、Λ は宇宙項、Tμν はエネルギー・運動量テンソルである。非相対論的極限でニュートンの重力理論に収束することから、右辺の比例係数 κ （アインシュタインの定数）は、



κ=8πGc4{displaystyle kappa ={frac {8pi G}{c^{4}}}}kappa ={frac {8pi G}{c^{4}}}



となる。G は万有引力定数、 c は光速である。4次元空間を考えれば、テンソルは対称なので、アインシュタイン方程式は、10本の方程式からなる。


アインシュタイン方程式の左辺は時空の曲率を表し、右辺は物質分布を表す。右辺の物質分布の項により時空が曲率を持ち、その曲率の影響で次の瞬間の物質分布が定まる、という構造である。真空の時空であれば、右辺をゼロとすればよい。例えば、重力以外の力を考えないと、次のようになる。



右辺のエネルギー運動量テンソルが増加の場合（アインシュタインの特殊相対論によるとエネルギーと質量は等価であるから、エネルギー運動量テンソルの増加は質量の増加を意味する）、左辺も増加しなければならない。これは時空の曲率が増加することを意味する。アインシュタインの解釈によると重力とは時空の湾曲によるものであったから、曲率の増加は重力の増大を表す。右辺のエネルギー運動量テンソルの増大は質量が増大する事を表し、この方程式によると、それは左辺の時空の曲率、つまり重力がさらに増大することを意味する。



すなわち、重力は非線形で、重力自身は自己増大してゆく。通常の恒星のモデルでは、核融合による、生じる光（電磁波）の輻射圧とガスによる圧力が、重力と釣り合うように恒星の半径が決まる。星が燃え尽きて支える力がなくなると、重力崩壊し、電子の縮退圧で支えられる白色矮星 か、中性子の縮退圧で支えられる中性子星、あるいは、ブラックホールになることが予測される。


アインシュタイン方程式の数学的な特徴は、次のような点にある。




  • 座標変換に対し、共変的であるので、「時間座標1＋空間座標3」のみではなく、「光の進行方向2＋空間座標2」といった分解表現も可能である。

  • 非線形の2階の偏微分方程式（楕円型偏微分方程式および双曲型偏微分方程式）である。

  • 時空構造を論じていながら、時空全体の大域的構造やトポロジーを仮定しない。

  • 得られる解には、特異点が存在する（特異点定理）。



アインシュタイン方程式の厳密解


アインシュタイン方程式自身に何ら近似することなく得られる解析解のことを厳密解という。良く知られている厳密解に、次のものがある。



シュヴァルツシルト解


カール・シュヴァルツシルトが1916年に発表した解。真空で球対称を仮定した解で、ブラックホールを表す最も単純な解。

カー解


ロイ・カーが1962年発表した解。真空で軸対称時空を仮定した解で、回転するブラックホールを表す最も単純な解。

ドジッター解


ウィレム・ド・ジッターが1917年に発表した解。真空で宇宙項がある場合の膨張宇宙解。ド・ジッター宇宙を表す。

フリードマン・ロバートソン・ウォーカー解


アレクサンドル・フリードマン、ハワード・ロバートソン、アーサー・ウォーカーが1922年に発表した解。時空の球対称性を仮定し、物質分布を一様等方な流体近似した解で、ビッグバン膨張宇宙を表す解。

ゲーデル解


クルト・ゲーデルが1949年に発表した解。物質分布を規定するエネルギー・運動量テンソルを、回転する一様なダスト粒子として仮定し、ゼロでない宇宙項を仮定した解で、ゲーデルの回転宇宙を表す解。


現在でも、新しい解（解析解）を発見すれば、発見者の名前がつく。ただし、同じ物理的な時空であっても、異なる座標表現を用いて、異なる解のように表現されることがあるので、注意することが必要である。



一般相対性理論の応用



GNSS


自動車などの位置をリアルタイムに測定表示するカーナビゲーションシステムは、GNSSの代表といえるGPSなどを利用しており、GPS衛星などに搭載された原子時計に基づき生成される航法信号に依存している。


GPS衛星からの信号を受信する装置では、さまざまな要因による補正を行うが、GPS衛星の時計との同期に関するものとして、地表に対して高速で運動するGPS衛星の、特殊相対論効果による地表からみた時間の遅れ、および地球の重力場による地上の時間の遅れ、言い換えれば一般相対論効果による衛星の時計の進みが含まれる[注 11]。


GPS衛星の軌道速度は秒速約4キロメートルと高速であるため、特殊相対論によって時間の進み方がわずかではあるが遅くなる。一方、GPS衛星の高度は約2万キロメートルで、地球の重力場の影響が小さいことから、一般相対論によって地上よりも時間の進み方が速くなる。このように特殊相対論と一般相対論で互いに逆の効果をもたらすことになる。この相対論的補正をせずに1日放置すると、位置情報が約11キロメートルもずれてしまうほどの時刻差になることから、相対論的補正はGPSシステムの運用に不可欠である[8]。



脚注


[ヘルプ]


注釈





  1. ^ レフ・ランダウは、一般相対論は現存する物理学の理論の中で最も美しい理論だと述べている。


  2. ^ 原題：Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes


  3. ^ 原題：Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation


  4. ^ 原題： Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. Bibcode 1915SPAW.......831E. doi:10.1002/3527608958.ch4. .


  5. ^ 原題：Die Grundlage der allgemeinen Relativitätstheorie


  6. ^ 原題： Hamiltonsches Prinzip und allgemeine Relativitätstheorie. Bibcode 1916SPAW......1111E. doi:10.1002/3527608958.ch9. 


  7. ^ 一般共変性の仮定においては『自然の一般法則』であり『物理法則』ではない。


  8. ^ 重力場がある場合は、等価原理により、座標系の加速状態を適当に選ぶことで、特殊相対性理論が成り立つ座標系を取ることができる[4]。


  9. ^ 通常、数学でリーマン多様体というとユークリッド空間をパッチワークのように張り合わせたものを指し、2点間の距離の2乗が非負の正定値計量と呼ばれる空間である。それに対して、一般相対性理論が扱うのは、時間と空間の意味をもつ座標を含むミンコフスキー空間を張り合わせたものであり、2点間の距離が虚数になり得る不定計量の空間である。このため、擬リーマン多様体 (pseudo-Riemannian manifold) とも呼ばれる。


  10. ^ これをミンコフスキー計量 (metric) と呼ぶこともある。


  11. ^ 他に地球自転に起因する信号伝播に対するサニャック効果もある。




出典





  1. ^ 選集2 [A2]一般相対性理論および重力論の草案 (1914), p.34


  2. ^ リーマン幾何とその応用 (1971), p. 100.


  3. ^ リーマン幾何とその応用 (1971), p. 104.


  4. ^ リーマン幾何とその応用 (1971), pp. 105-107.


  5. ^ リーマン幾何とその応用 (1971), p. 106.


  6. ^ リーマン幾何とその応用 (1971), p. 117.


  7. ^ リーマン幾何とその応用 (1971), p. 105.


  8. ^ Neil Ashby (2002年5月). “Relativity and the Global Positioning System”. Physics Today (American Institute of Physics) 55 (5): 41. doi:10.1063/1.1485583. 




参考文献




  • A. Einstein (1911年6月21日). “Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes [光の伝播に対する重力の影響]” (German) (PDF). Annalen der Physik (Leipzig) 340 (10): 898-908. Bibcode 1911AnP...340..898E. doi:10.1002/andp.19113401005. ISSN 0003-3804. OCLC 5854993. http://www.itp.kit.edu/~sahlmann/pdfs/propagation%20of%20light.pdf. 


  • A. Einstein (1916年3月20日). “Die Grundlage der allgemeinen Relativitätstheorie [一般相対性理論の基礎]” (German) (PDF). Annalen der Physik (Leipzig) 354 (7): 769–822. Bibcode 1916AnP...354..769E. doi:10.1002/andp.19163540702. ISSN 0003-3804. OCLC 5854993. http://www.physik.uni-augsburg.de/annalen/history/einstein-papers/1916_49_769-822.pdf. 

  • 内山龍雄 『相対性理論』 岩波書店〈物理テキストシリーズ8〉、1987年1月29日。全国書誌番号:87019979。ISBN 4-00-007748-1。NCID BN00639508。OCLC 673778932。ASIN 4000077481。

  • P.A.M.Dirac 『一般相対性理論』 江沢洋訳、筑摩書房〈ちくま学芸文庫〉、2005年12月。全国書誌番号:20969268。ISBN 4-480-08950-0。NCID BA74624119。OCLC 674910090。ASIN 4480089500。

  • フィリップ・フランク 『評伝 アインシュタイン』 矢野健太郎訳、岩波書店、2005年。

  • リーマン、リッチ、レビ=チビタ、アインシュタイン、マイヤー 『リーマン幾何とその応用』 矢野健太郎訳、共立出版、1971年。

  • メラー 『相対性理論』 永田 恒夫, 伊藤 大介訳、みすず書房、1959年。

  • 矢野 健太郎 『アインシュタイン』、1991年。

  • 矢野 健太郎 『微分幾何学』 朝倉書店、1949年。

  • 矢野 健太郎 『接続の幾何学』 河出書房、1948年。

  • 矢野 健太郎 『リーマン幾何学入門』 森北出版、1971年。

  • 坪井 忠二 『重力』 岩波全書、1979年、第2版。

  • ア・グリゴリヤン 『力学はいかに創られたか』 小林 茂樹、今井 博訳、東京図書株式会社、1970年。

  • シュポルスキーほか 『アインシュタインと現代物理学』 東京図書株式会社、1958年。



関連文献



  • A.Einstein 『アインシュタイン選集1――特殊相対性理論・量子論・ブラウン運動――』 中村誠太郎・谷川安孝・井上健訳・編、湯川秀樹監修、共立出版、1971年3月1日。全国書誌番号:69018983。ISBN 978-4-320-03019-0。NCID BN00729724。OCLC 834568557。ASIN 4320030192。

  • A.Einstein 『アインシュタイン選集2――一般相対性理論および統一場理論――』 内山龍雄訳・編、湯川秀樹監修、共立出版、1970年12月5日。全国書誌番号:69018984。ISBN 978-4-320-03020-6。NCID BN00963834。OCLC 834568671。ASIN 4320030206。

  • A.Einstein 『アインシュタイン選集3――アインシュタインとその思想――』 中村誠太郎・井上健訳・編、湯川秀樹監修、共立出版、1972年1月25日。全国書誌番号:69018985。ISBN 978-4-320-03021-3。NCID BN00729768。OCLC 834568753。ASIN 4320030214。

  • 内山龍雄 『一般相対性理論』 裳華房〈物理学選書15〉、1978年7月30日。全国書誌番号:78026559。ISBN 978-4-7853-2315-8。NCID BN00729054。OCLC 873890979。ASIN 4785323159。

  • 佐藤勝彦 『相対性理論』 岩波書店〈岩波基礎物理シリーズ9〉、1996年12月18日。全国書誌番号:97049882。ISBN 4-00-007929-8。NCID BN15591416。OCLC 675345203。ASIN 4000079298。

  • 佐藤文隆、小玉英雄 『一般相対性理論』 岩波書店〈現代物理学叢書〉、2000年6月15日。全国書誌番号:20086007。ISBN 4-00-006742-7。NCID BA47513104。OCLC 54548828。ASIN 4000067427。

  • W.Pauli 『相対性理論』上巻、内山龍雄訳、筑摩書房〈ちくま学芸文庫〉、2007年12月10日。全国書誌番号:21355333。ISBN 978-4-480-09119-2。NCID BA84202329。OCLC 675553164。ASIN 448009119X。

  • W.Pauli 『相対性理論』下巻、内山龍雄訳、筑摩書房〈ちくま学芸文庫〉、2007年12月10日。全国書誌番号:21355334。ISBN 978-4-480-09120-8。NCID BA84202329。OCLC 675553100。ASIN 4480091203。

  • L.D. Landau、E.M. Lifshitz 『場の古典論――電気力学、特殊および一般相対性理論』 恒藤敏彦・広重徹訳、東京図書〈ランダウ=リフシッツ理論物理学教程 第2巻〉、1978年10月、原書第6版。全国書誌番号:79000237。ISBN 978-4-489-01161-0。NCID BN00890297。OCLC 841897028。ASIN 448901161X。


  • W. Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (September 15, 1973). Gravitation. Physics Series. W H Freeman & Co (Sd). ASIN 0716703440. ISBN 0-7167-0344-0. NCID BA00053088. OCLC 585119. 


  • Wald, Robert (June 15, 1984). General Relativity. Univ of Chicago Pr (Tx). ASIN 0226870332. ISBN 0-226-87033-2. NCID BA00907886. OCLC 10018614. ASIN B004DL0OEO (Kindle). 



関連項目





ウィキブックスに一般相対性理論関連の解説書・教科書があります。



  • アインシュタイン方程式 - エネルギー・運動量テンソル

  • アルベルト・アインシュタイン


  • 宇宙論 - ビッグバン - インフレーション宇宙 - 宇宙背景輻射


  • シュヴァルツシルトの解 - ライスナー・ノルドシュトロム解 - カー解 - カー・ニューマン解 - フリードマン・ロバートソン・ウォーカー計量 - ゲーデル解

  • 重力子

  • 重力相互作用

  • 重力波

  • サニャック効果

  • 数値相対論


  • 相対性理論 - 特殊相対性理論

  • 微分幾何学


  • ブラックホール - シュヴァルツシルト・ブラックホール - カー・ブラックホール


  • ポスト・ニュートン展開 - PPN形式

  • リーマン幾何学


  • 量子重力理論 - 超弦理論 - M理論

  • ワームホール

  • 1919年5月29日の日食



外部リンク



  • ブリタニカ国際大百科事典 小項目事典『一般相対性理論』 - コトバンク


  • General relativity - ブリタニカ百科事典






























  • 表

  • 話

  • 編

  • 歴


物理学の分野
古典・量子



  • 古典物理学（古典論）

  • 半古典論


  • 量子物理学（量子論）
研究方法

  • 理論物理学

  • 計算物理学


  • 実験物理学（高エネルギー物理学）

    		•
    基礎理論

  • 力学


  • 古典力学

    • ニュートン力学

    • 解析力学



  • 連続体力学

  • 流体力学

  • 熱力学

  • 統計力学

  • 電磁気学

  • 量子力学

  • 相対論的量子力学

  • 場の量子論


  • 相対性理論

    • 特殊相対性理論

    • 一般相対性理論



    		•
    研究対象

  • 素粒子物理学


  • 原子核物理学

    • 核構造物理学

    • ハドロン物理学




  • 宇宙物理学
    • 宇宙論



  • 物性物理学

    • 固体物理学

    • 表面科学

    • 低温物理学

    • ソフトマター物理学

    • 高分子物理学



  • 原子物理学

  • 分子物理学

  • 光学

  • 音響学

  • プラズマ物理学

    		•
    境界領域

  • 数理物理学

  • 化学物理学

  • 生物物理学


  • 地球物理学

    • 大気物理学

    • 海洋物理学




  • 農業物理学
    • 土壌物理学


  • 医学物理学

  • 保健物理学

  • 放射線物理学

  • 経済物理学

    		•
    その他

  • 現代物理学

  • 応用物理学

  • 物理数学

    		•


















    • 表

    • 話

    • 編

    • 歴


    相対性理論
    特殊
    相対論























    背景


    • 相対性原理

    • 特殊相対性理論
    基礎

  • 相対運動

  • 基準系

  • 光速

  • マクスウェルの方程式

    		•
    公式

  • ガリレイ相対性（英語版）

  • ガリレイ変換

  • ローレンツ変換

    		•
    結果

  • 時間の遅れ

  • 相対論的質量（英語版）

  • E = mc2

  • 長さの短縮（英語版）

  • 同時性の相対性（英語版）

  • 相対論的ドップラー効果（英語版）

  • トーマス歳差（英語版）

  • 相対論的ディスク（英語版）

    		•
    時空

  • ミンコフスキー時空

  • 世界線

  • ミンコフスキーダイアグラム（英語版）

  • 光円錐

    		•


    		Spacetime curvature.png
    一般
    相対論



























    背景


    • 一般相対論の数学

    • 関連文献
    基礎

  • 特殊相対性理論

  • 等価原理

  • 世界線

  • リーマン幾何学

  • ミンコフスキーダイアグラム（英語版）

    		•
    現象

  • 二体問題（英語版）

  • 重力レンズ

  • 重力波

  • 慣性系の引きずり

  • 測地的効果（英語版）

  • 事象の地平面

  • 重力の特異点

  • ブラックホール

    		•
    方程式

  • 線形化重力（英語版）

  • PPN形式

  • アインシュタイン方程式

  • 測地線方程式（英語版）

  • フリードマン方程式

  • ADM形式（英語版）

  • BSSN形式（英語版）

  • ハミルトン＝ヤコビ＝アインシュタイン方程式（英語版）

    		•
    発展
    理論

  • カルツァ＝クライン理論

  • 量子重力理論

  • ブランス＝ディッケ理論（英語版）

    		•
    解（英語版）

  • シュワルツシルト

  • ノルドシュトロム


  • ゲーデル
    カー

  • カー・ニューマン

  • カスナー（英語版）

  • タアブ・NUT（英語版）

  • ミルン（英語版）

  • フリードマン・ルメートル・ロバートソン・ウォーカー

  • pp-wave時空（英語版）

  • ファン・ストックム・ダスト（英語版）

    		•


    科学者

  • アインシュタイン

  • ローレンツ

  • ヒルベルト

  • ポアンカレ

  • シュヴァルツシルト

  • ド・ジッター

  • ライスナー

  • ノルドシュトルム

  • ワイル

  • エディントン

  • フリードマン

  • ミルン

  • ツビッキー

  • ルメートル

  • ゲーデル

  • ホイーラー

  • ロバートソン

  • バーディーン

  • ウォーカー

  • カー

  • チャンドラセカール

  • エーラス（英語版）

  • ペンローズ

  • ホーキング

  • テイラー

  • ハルス

  • ストックム（英語版）

  • タアブ（英語版）

  • ニューマン（英語版）

  • ヤウ

  • ソーン

  • ノッターレ（英語版）

  • その他（英語版）

    		•







































    • 表

    • 話

    • 編

    • 歴


    テンソル

    Glossary of tensor theory（英語版）
    範囲 (Scope)











    数学


    • 座標

    • 多重線型代数

    • ユークリッド幾何学

    • テンソル代数

    • 微分幾何学

    • exterior calculus

    • テンソル解析

    物理学 • 工学

  • 連続体力学

  • 電磁気学

  • 移動現象論

  • 一般相対性理論

  • コンピュータビジョン

    		•


    表記法 (Notation)

  • 添字表記法

  • 多重指数

  • アインシュタインの縮約記法

  • リッチ解析（英語版）

  • Penrose graphical notation（英語版）

  • フォークト表記（英語版）

  • 抽象添字記法

  • テトラド表記（英語版）

  • ファン・デル・ヴェルデン表示

    		•
    テンソルの定義

  • テンソル空間

  • テンソル場

  • テンソル密度（英語版）

  • 曲線座標系におけるテンソル（英語版）

  • 混テンソル（英語版）

  • 反対称テンソル

  • 対称テンソル

  • テンソル作用素（英語版）

  • テンソル束（英語版）

    		•
    算法

  • テンソル積

  • 楔積

  • テンソルの縮約

  • 行列（2階テンソル）の転置

  • 添字の上げ下げ（英語版）

  • ホッジ双対

  • 共変微分

  • 外微分

  • 共変外微分（英語版）

  • リー微分

    		•
    関連事項

  • 次元

  • 基底


  • ベクトル、ベクトル空間

  • 多重ベクトル（英語版）

  • ベクトルの共変性と反変性

  • 線型写像

  • 行列

  • スピノール

  • カルタン形式

  • 微分形式

  • 接続形式

  • 測地線

  • 多様体

  • ファイバー束

  • 曲率形式

  • レヴィ・チヴィタ接続

  • アフィン接続

    		•
    有名なテンソル











    数学


    • クロネッカーのデルタ

    • エディントンのイプシロン

    • 計量テンソル

    • クリストッフェル記号

    • リッチテンソル

    • リーマン曲率テンソル

    • ワイルテンソル（英語版）

    • 捩れテンソル
    物理学

  • 慣性モーメント

  • 角運動量

  • 応力テンソル

  • エネルギー・運動量テンソル

  • 電磁テンソル

  • グルーオン場の強度テンソル（英語版）

  • アインシュタインテンソル

  • 計量テンソル (一般相対論)（英語版）

    		•


    数学者

  • レオンハルト・オイラー

  • カール・フリードリヒ・ガウス

  • オーギュスタン＝ルイ・コーシー

  • ヘルマン・グラスマン

  • グレゴリオ・リッチ＝クルバストロ

  • トゥーリオ・レヴィ＝チヴィタ

  • Jan Arnoldus Schouten（英語版）

  • ベルンハルト・リーマン

  • エルヴィン・クリストッフェル

  • ヴォルデマール・フォークト

  • エリ・カルタン

  • ヘルマン・ワイル

  • アルベルト・アインシュタイン

    		•

    カテゴリCategory:テンソル

























    • 表

    • 話

    • 編

    • 歴


    アルベルト・アインシュタイン
    キャリア


    • 特殊相対性理論

    • 一般相対性理論

    • E = mc2

    • ブラウン運動

    • 光電効果

    • アインシュタイン係数（英語版）

    • アインシュタイン模型

    • 等価原理

    • アインシュタイン方程式

    • アインシュタイン半径（英語版）

    • アインシュタインの関係式

    • 宇宙定数

    • ボース＝アインシュタイン凝縮

    • ボース=アインシュタイン分布関数

    • ボース＝アインシュタイン相関（英語版）

    • アインシュタイン＝カルタン理論（英語版）

    • アインシュタイン＝インフェルト＝ホフマンの方程式（英語版）

    • アインシュタイン＝ド・ハース効果（英語版）

    • EPRパラドックス

    • EBK量子化条件

    • アインシュタインとボーアのディベート（英語版）

    • 遠隔平行性（英語版）

    • アインシュタインの成功しなかった研究（英語版）
    著作物（英語版）

  • アインシュタインの原論文


  • ブラウン運動の理論 (1905)


  • 運動物体の電気力学について (1905)


  • 特殊および一般相対性理論について (1916)


  • わが世界観（英語版） (1949)


  • 私の社会主義（英語版） (1949)


  • ラッセル＝アインシュタイン宣言 (1955)

    		•
    家族（英語版）


  • パウリーネ・コッホ（英語版） (母)


  • ヘルマン・アインシュタイン（英語版） (父)


  • マヤ・アインシュタイン（英語版） (妹)


  • ミレヴァ・マリッチ (1人目の妻)


  • エルザ・アインシュタイン (2人目の妻)


  • リーゼル・アインシュタイン（英語版） (娘)


  • ハンス・アルベルト・アインシュタイン (息子)


  • エドゥアルト・アインシュタイン (息子)


  • ベルンハルト・ツェーザー・アインシュタイン（英語版） (孫)


  • イブリン・アインスタイン（英語版） (孫)


  • トーマス・マーチン・アインスタイン（英語版） (ひ孫)

    		•
    アインシュタイン賞

  • アルベルト・アインシュタイン賞

  • アルベルト・アインシュタイン・メダル

  • アルベルト・アインシュタイン平和賞（英語版）

  • アルベルト・アインシュタイン世界科学賞

  • アインシュタイン賞 (APS)

  • レーザー科学アインシュタイン賞

    		•
    その他

  • 政治観（英語版）

  • 宗教観（英語版）

  • アルベルト・アインシュタインの家（英語版）

  • アインシュタインの冷蔵庫

  • 脳（英語版）

  • 大衆文化におけるアルベルト・アインシュタイン（英語版）

  • アインスタイニウム

  • アインシュタインの受賞・受勲暦（英語版）

  • アルベルト・アインシュタインの名に由来するものの一覧（英語版）

  • アインシュタイン・ペーパーズ・プロジェクト（英語版）

    		•








    -

    Popular posts from this blog

    Full-time equivalent

    Image
    Full-time equivalent From Wikipedia, the free encyclopedia Jump to navigation Jump to search Full-time equivalent ( FTE ) or whole time equivalent ( WTE ) is a unit that indicates the workload of an employed person (or student) in a way that makes workloads or class loads comparable [1] across various contexts. FTE is often used to measure a worker's or student's involvement in a project, or to track cost reductions in an organization. An FTE of 1.0 is equivalent to a full-time worker or student, while an FTE of 0.5 signals half of a full work or school load. [2] Contents 1 U.S. Federal Government 2 In education 2.1 Example 3 Notes 4 References U.S. Federal Government [ edit ] In the U.S. Federal Government, FTE is defined by the Government Accountability Office (GAO) as the number of total hours worked divided by the maximum number of compensable hours in a full-time schedule as...
    Read more

    さくらももこ

    Image
    さくら ももこ 本名 非公開 [1] 生誕 ( 1965-05-08 ) 1965年5月8日 日本・静岡県清水市 （現・静岡市清水区） 死没 ( 2018-08-15 ) 2018年8月15日（53歳没） 日本・東京都目黒区 国籍 日本 職業 漫画家 エッセイスト 作詞家 活動期間 1984年 - 2018年 ジャンル 少女漫画 青年漫画 児童漫画 代表作 『ちびまる子ちゃん』 『コジコジ』 受賞 1989年：第13回講談社漫画賞少女部門 （『ちびまる子ちゃん』） 1990年：第32回日本レコード大賞 （『おどるポンポコリン』作詞） 公式サイト さくらプロダクション テンプレートを表示 さくら ももこ （1965年5月8日 - 2018年8月15日 [2] ）は、日本の漫画家、エッセイスト、作詞家、脚本家。また、自身の少女時代をモデルとした代表作のコミック『ちびまる子ちゃん』の主人公の名前でもある。静岡県清水市（現・静岡市清水区）出身。血液型はA型。身長159cm。一男の母親。 代表作のコミック『ちびまる子ちゃん』の単行本の売上は累計3000万部を超える。また、エッセイストとしても独特の視点と語り口で人気が高く、初期エッセイ集三部作『もものかんづめ』『さるのこしかけ』『たいのおかしら』はいずれもミリオンセラーを記録。 目次 1 経歴 2 人物・交遊関係 3 主な作品 3.1 漫画 3.2 エッセイ 3.3 作詞 3.4 詩集 3.5 雑誌・ムック本 3.6 翻訳 3.7 絵本、ドラマ脚本他 3.8 ラジオ出演 3.9 その他 4 関係人物 4.1 アシスタント 4.2 さくらももこを演じた人物 5 脚注 5.1 注釈 5.2 出典 6 外部リンク 経歴 年譜形式の経歴は推奨されていません 。人物の伝記は流れのあるまとまった文章で記述し、年譜は補助的な使用にとどめてください。 （ 2018年8月 ） 清水市立（当時）入江小学校...
    Read more

    13 indicted, 8 arrested in Calif. drug cartel investigation

    Image
    Fox News U.S. World Opinion Politics Entertainment Business Lifestyle TV Radio More Expand / Collapse search Login Watch TV ☰ Hot Topics U.S. Crime Military Education Terror Immigration Economy Personal Freedoms World U.N. Conflicts Terrorism Disasters Global Economy Environment Religion Scandals Opinion Politics Executive Senate House Judiciary Foreign policy Polls Elections Entertainment Celebrity News Movies TV News Music News Style News Entertainment Video Business Markets Politics Technology Features Business Leaders Lifestyle Food + Drink Cars + Trucks Travel + Outdoors House + Home Fitness + Well-being Style + Beauty Family Science Archaeology Air & Space Planet Earth Wild Nature Natural Science Dinosaurs Tech Security Innovation Drones Computers Video Games Military Tech Health Healthy Living Medical Research Mental Health Cancer Heart Health Children'...
    Read more